
介绍
在过去的二十年里,砷的化合物因其在古代被用作颜料,以及在现代工业中被用作改变铅和铜合金机械性能的成分,以及消除玻璃中不想要的色素的成分,而受到实验和理论上的研究。1,2 砷簇不仅在早期法医学和化疗的发展中发挥了重要作用,而且在现代科学的许多不同领域,如固体物理学、生物化学、物理化学、表面现象和催化等领域中也扮演着重要角色。1-17 关于其基本性质的知识,如中性及带电砷簇的基态和低能电子态、电子亲和能(EA)以及电离能(IP),应有助于更全面地理解其在不同领域中的作用。基于这一动机,我们利用更高阶的Gaussian-3(G3)理论,对中性及带电砷簇的结构和性质进行了详细的研究。18,19
关于砷簇的实验研究已有先例。例如,Bennett等人12测量了负离子As-的电势和离子平动能量,
As²和As³通过As⁴的解离共振捕获形成。利帕克特尔团队于1998年利用光电子能谱研究了Asn(n=1-5)的电子结构和电子关联。2002年,翟等人通过光电子能谱与从头计算研究了Pn⁵(Pn为磷、砷、锑、铋)的电子结构及电子关联。近期,沃尔特团队采用红外光电子脱离阈值光谱法测定了砷原子的结合能和精细结构分裂。针对砷离子团簇,巴蒂亚和琼斯通过光学光谱测量了其电子结构。齐默尔曼团队利用气相电荷转移反应确定了砷团簇(Asn,n=1-5)的电子结构。王等人通过高分辨率光电子能谱与光电离质谱分别测定了As²和As⁴的电子结构,柳等人则通过光致电离质谱实现了As4的电子结构测定。布伦巴赫与罗森布拉特运用拉曼光谱研究了As⁴的振动模式。
研究砷化物簇(特别是n≤6的小型簇)的结构与性质存在多种方法。例如,Scu-seria25团队采用CCSD方法对As2进行了键长、谐波振动频率及红外光谱的研究。Balasubramanian等人通过CAS-MCSCF,followedbyMRCI.Meieretal.26结构分析,系统探讨了As3及其正离子的电子结构和势能面。
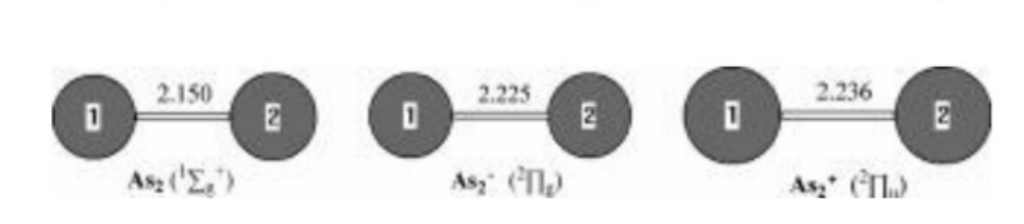
图1.采用MP2(全)方案和6-31G(d)基组优化的中性及带电As₂0-1-1)几何结构。键长单位为埃。
在MRDCI理论水平下,研究了As2和As4的稳定性及电离势。Warren等人27通过abinitioSCF-MO计算研究了As6的几何结构。BelBruno28使用B3PW91方案探索了Asn(n=2-5)团簇的成键特性。Igel-Mann等29利用自洽场和CI方法结合能量调整赝势,探究了Asn(n=1-6)的结构和垂直电荷势。Zhao等人8采用多种密度泛函理论(DFTs)研究了Asn(n=1-5)的结构和电子势。对于中型Asn团簇,Ballone等人30使用局域和非局域密度泛函研究了Asn团簇up至t=11的结构。Zhao等人7报告了在n≤28范围内使用双数值加d极化(DND)型全电子基组的DFT与PBE交换关联泛函对Asn团簇结构和电子性质的研究。Guo6利用B3LYP/6-311+G(d)方法研究了n=2-15中性及带电Asn团簇的几何与电子性质。此外,Schae-fer及其同事9使用HF、MP2、CISD和CCSD方法研究了n=2、4、12和20的Asn团簇稳定性。Baruah等人31通过广义梯度近似(GGA)方法,探索了n=4、8、20、28、32、36和60的类富勒烯砷笼的几何结构、极化率以及红外和拉曼光谱。
本研究旨在运用更高级别的G3理论来确定天冬酰胺(n=2-8)物种的电子自旋态(EAs)及其他性质。具体目标包括:(a)将电子自旋态与有限的实验数据进行对比;(b)预测其他性质参数,如离子化势、结合能及多种解离能。在缺乏实验数据的情况下,我们致力于为这些砷簇建立可靠的理论预测模型,并在某些情况下对现有实验结果提出挑战。
计算方法
G3理论延伸处的所有计算
我们使用Gaussian03软件包完成了ry18和ry19的计算。32综合应用G3方法进行的从头算研究,针对含第一、第二及第三周期元素的化合物分子能量展开分析。在包含生成焓、电离势、电子a区nities和质子a区nities等参数的423个反应中,平均绝对偏差与实验值的吻合度达到1.06千卡/摩尔。19最近我们采用该G3理论计算了Sin簇(n≤10)的电子能量,结果显示其平均绝对偏差仅为0.97千卡/摩尔(0.042电子伏特)。33
结果和讨论
砷化二硫化物及其带电分子。图1展示了砷化二硫化物基态及其带电态的优化几何结构。在12g+基态中,实验测得的砷-砷键长为2.103埃。34通过MP2(全)/6-31G(d)方法预测的砷-砷键长为2.150埃,该数值比实验值高估了0.047埃。而CCSD方法给出的最佳理论预测值为2.107埃。
表1.酪氨酸(n=2-8)的零点振动能量(ZPVE)校正绝热电子势(EAs)与绝热电离势(IPs)a
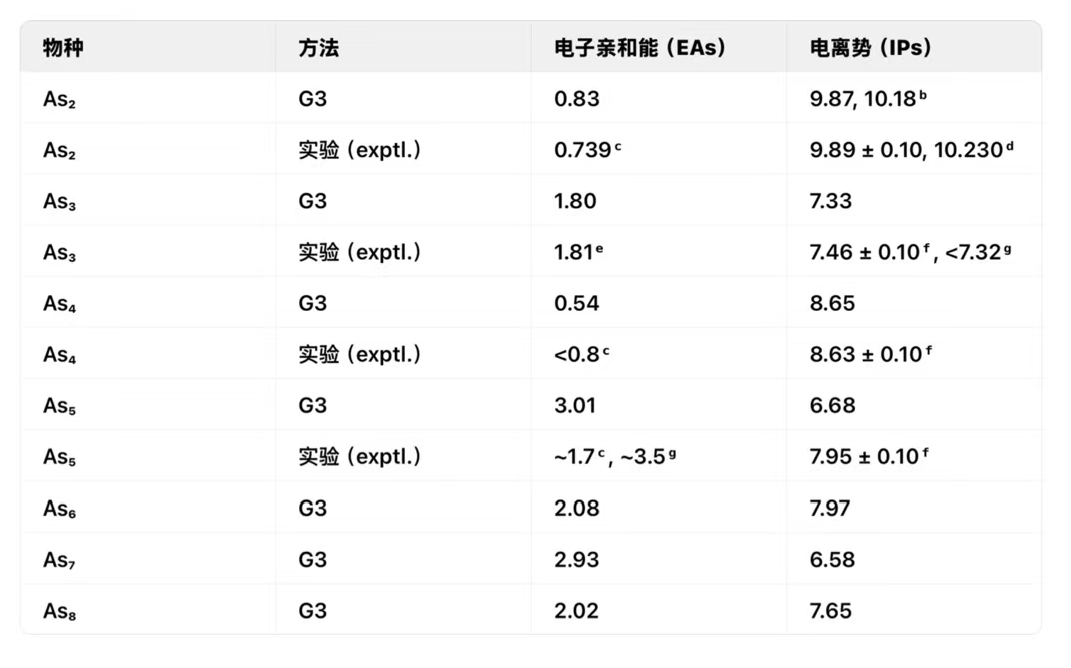
a 以电子伏特(eV)表示。b 对于¹Σ₉⁺ f ²Πᵤ为9.87 eV,对于¹Σ₉⁺ f ²Σ₉⁺为10.18 eV。c 参考文献1。d ¹Σ₉⁺ f ²Πᵤ的9.89±0.1 eV取值来自参考文献3,¹Σ₉⁺ f ²Σ₉⁺的10.230 eV取值来自参考文献21。e 我们重新指认了Lippa等人记录的光电子能谱(见参考文献1),并得到As₃(²B₁ ← ³A₁⁰)的实验值为1.81 eV;见正文。f 参考文献3。g 参考文献4。
由斯库塞里亚(Scuseria)等人报告的值为……(此处原句“reported by Scuseria et al.25”中数字25表意不明,推测可能是文献引用编号),沈(Shen)等人报告的值为2.099埃。耦合簇单双激发(CCSD)计算结果与实验值的偏差仅为±0.004埃。
阴离子As₂⁻在其²Πg基态下,实验测得的As - As键长为2.239埃。二阶微扰理论(MP2(full)/6 - 31G(d))计算结果为2.225埃,与实验值相当吻合,与实验值的偏差仅为0.014埃。我们注意到,采用DZP++基组的BP86和BLYP方法的理论计算结果与实验值相符。预测As₂的电子亲和能(EA)为0.83电子伏特(n = 2 - 8的Asₙ的理论和实验电子亲和能及电离能列于表1),这与光电子能谱测量得到的实验值0.739电子伏特相符。
阳离子As₂⁺具有²Πu基态和一个低激发态²Σg。在G3理论水平下,后一激发态的能量比基态高0.33电子伏特。预测²Πu态下As - As键长为2.236埃,²Σg态下为2.143埃。采用G3方法并考虑零点振动能(ZPVE)校正计算得到的电离能(IP):从¹Σg⁺到²Πu为9.87电子伏特,从¹Σg⁺到²Σg⁺为10.18电子伏特,这与实验值9.893和10.23电子伏特非常吻合。
As3 及其带电分子。图 2 展示了中性 As3 的四种极小结构、阴离子 As3 - 的两种极小结构和阳离子 As3 + 的一种极小结构。从图 2 可以看出,中性 As3 的三种等腰三角形结构的电子态分别为 2B1、2A2 和 2A1 态。从能量上看,能量最低的 2B1 结构比 2A2 和 2A1 结构分别稳定 0.04 eV 和 1.77 eV。第四种异构体,即线性结构,具有 2Ig 电子态。从能量上看,它比 2B1 结构高 1.53 eV。我们注意到,在 Zhao 等人[8]和 Balasubramanian 等人[11]分别报道的各种密度泛函理论(DFT)和完全活性空间自洽场/多参考态单双激发组态相互作用(CASSCF/MRSDCI)水平下,2A2 态在能量上比 2B1 态稳定 0.02 - 0.05 eV。这意味着 2B1 和 2A2 电子态在竞争 As3 的基态。我们还注意到,Guo[6]报道 As3 的基态是线性结构。
对于阴离子 As3 - 的基态结构,Zhao 等人[8]预测它是具有 C2v 对称性和 1A1 电子态的等腰三角形。Guo[6]预测它是等边三角形。
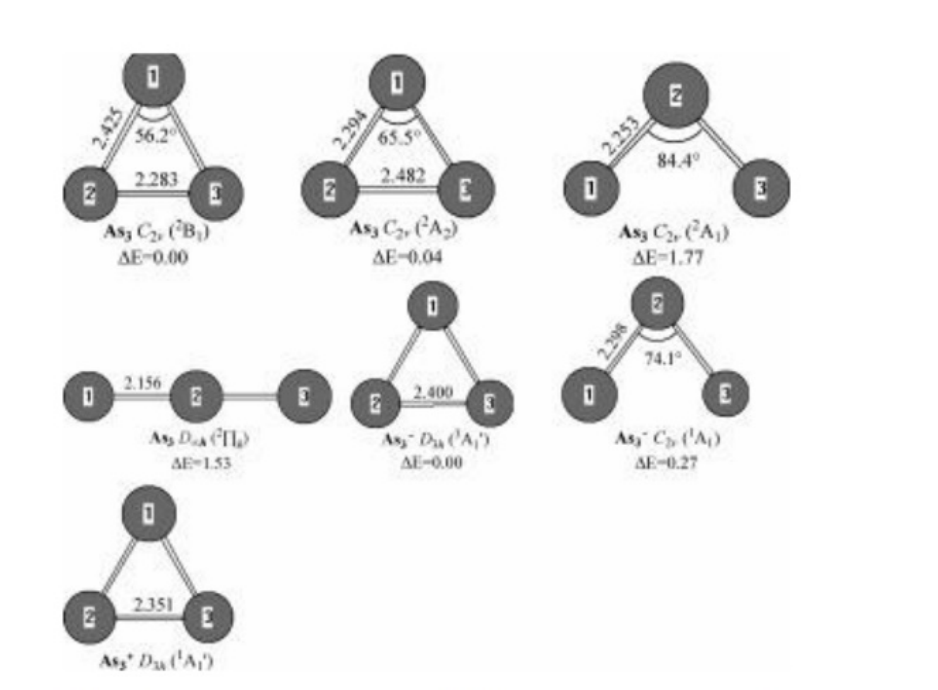
图2.采用MP2(全电子)方法和6 - 31G(d)基组优化得到的中性和带电的As₃(0, - 1, + 1)几何结构。键长和键角的单位分别为埃和度。相对能量ΔE是在G3水平下获得的,未进行零点振动能(ZPVE)校正,单位为电子伏特(eV)
具有D₃h对称性和³A₁′电子态。在G3水平下,³A₁′态结构在能量上比¹A₁态稳定0.27 eV。通过G3方法预测,对于²B₁ + ³A₁′,电子亲和能(EA)为1.80 eV;对于²B₁ + ¹A₁,电子亲和能为1.54 eV。Lippa等人[1]获得了As₃⁻的光电子能谱,有两个主要谱带标记为A和B。Lippa等人[1]将谱带A归因于阴离子基态与As₃的²A₂基态之间的跃迁,将谱带B归因于阴离子基态与As₃的²B₁态之间的跃迁,并得出As₃的电子亲和能为1.45 ± 0.03 eV,且²A₂和²B₁异构体之间的能隙为0.36 eV。实际上,如上文所述,用各种理论方法计算得到的²A₂和²B₁异构体之间的理论能隙仅为0.05 eV。因此,对As₃⁻光电子能谱的归属被认为是不合理的。在这种情况下,我们大胆地重新对能谱中的两个主要谱带进行归属(见参考文献1)。我们将谱带A归因于阴离子As₃⁻的¹A₁态与中性As₃的²B₁(或²A₂)基态之间的跃迁,将谱带B归因于阴离子As₃⁻的³A₁′基态与中性As₃的²B₁(或²A₂)基态之间的跃迁。由此测得As₃的实验电子亲和能对于²B₁ ← ¹A₁为1.45 eV,对于²B₁ ← ³A₁′为1.81 eV。测得As₃⁻的³A₁′和¹A₁异构体之间的能隙为0.36 eV。所有这些结果分别接近G3理论值1.54 eV、1.80 eV和0.27 eV。这一事实表明我们对光电子能谱的归属可能是合理的。
对于带正电的离子 As3+,预测其基态结构是具有 1A1' 态的等边三角形。这一结果与巴拉苏布拉马尼亚姆等人[11]和郭[6]先前报道的结果相同。预测其 G3 电离能为 7.33 电子伏特,这与理论值 7.1 电子伏特[11]以及实验值 7.49±0.13 电子伏特和小于 7.32 电子伏特[10]非常吻合。
As4 及其带电分子。已有大量关于 As4 的实验和理论研究。其中一个原因是,四面体 As4 结构是

图1.采用MP2(全)方案和6-31G(d)基组优化的中性及带电As₂9-1、+1)几何结构。键长单位为埃。
在大多数升华条件下,元素砷主要以四面体结构存在。先前研究[2,6-9,29-31]表明,As4在其1A1基态中呈现四面体分子构型。通过高温气相电子衍射技术,实验测得As-As键长为2.435±0.04 A。图3展示了中性As4、阴离子As4-和阳离子
As4+的G3几何构型。如图所示,采用MP2(全)/6-31G(d)能级计算得到的As-As键长2.444A,与文献[35]中2.435 A的实验值吻合度良好。 阴离子As4的对称基态结构与2B2电子态对称性相关。通过G3方案预测其电子能量为0.54 eV。赵等人计算得出电子能量应0.49,0.50,0.62为0.54 eV,而采用BLYP、BHLYP、B3LYP和BP86方法结合DZP++基组set,respectively.Lippaetal.1评估光电子能谱时,将As4的电子能量上限定为<0.8 eV。G3电子能量结果接近DFT计算值且低于上限值。
对于带正电的离子As4+,其基态结构呈现出D2d对称性,并包含2A1电子态。这一结论与B3LYP/
6-311+G(d)方法得出的结论存在差异。在B3LYP/6-311+G(d)计算水平下,基态
As4+结构在2B2态下展现出C2v对称性。理论预测的电负性为8.65电子伏特,与实验值8.63±0.1电子伏特高度吻合。我们注意到Wanget等人通过Jahn-Teller光谱模拟,在(1e)-1情况下对As4的电负性估计为7.83电子伏特。
As2-4的实验电子自旋(EAs)和离子对(IPs)可作为验证G3理论方法准确性的关键基准。针对六个反应体系(含两个电子自旋As2和As3,以及四个离子对As2、As3和As4),其与实验数据的平均绝对偏差仅为0.05电子伏特。关于As5及其带电分子结构的研究,目前仅有少量基于密度泛函理论(DFT)方案的理论成果。DFT计算表明,As5基团的最低能量同位素异构体具有C2v对称性,对应2B1态。图4所示的G3计算结果与先前DFT结论完全一致。 对于阴离子As5物种,图4所示的最低能量结构显示出D5h对称性与1A10电子态。这些结果与先前研究一致。4,6,8与中性As5相比,阴离子在几何构型上存在显著变化。G3预测的电子稳定能为3.01 eV,这是本文报道的所有方法中数值最大的。阴离子As5异常稳定的电子特性不仅归因于其闭壳层结构,还与其芳香特性有关。4 G3预测的As5电子稳定能接近BHLYP、B3LYP、BP86和BLYP方案的估算值(计算结果分别为2.92,3.14,3.12和3.03 eV)。8这种现象


实验值约1.71 eV和~3.51 eV之间存在较大差异。4 约1.7 eV的电子亲和能(EAs)是通过用2.497 eV光子进行的光电子能谱测量得到的。1 如果G3方法计算得到的3.01 eV的值是可靠的,那么约1.7 eV的实验值可能由于光子能量不足而不准确。翟等人4 记录了用4.661 eV和6.424 eV光子得到的两个光电子能谱。根据4.661 eV光子的光电子能谱,确定电子亲和能为3.51 eV。尽管这些实验值与B3P86和LSDA方法预测的值(B3P86和LSDA计算的电子亲和能分别为3.55 eV和3.54 eV)非常吻合,8 但B3P86和LSDA方法的结果往往会高估实验值。36 在参考文献36中,里恩斯特拉 - 基拉科菲等人回顾了用六种密度泛函理论(DFT)方法(B3LYP、B3P86、BHLYP、BLYP、BP86和LSDA)对电子亲和能的理论预测,并表明B3P86和LSDA方法对近110种物质的电子亲和能的平均高估误差超过0.6 eV。所有这些都表明,对于As₅,G3方法计算得到的3.01 eV的电子亲和能是可靠的。
对于阳离子As5+物种,其最低能量结构具有C4v对称性并呈现1A1基态。这一结果与先前研究结论一致。6通过对比中性As5发现,阴阳离子在几何构型上存在显著差异。理论预测的电离势(IP)值为6.68电子伏特(G3水平)。值得注意的是,该理论IP值与实验测量值7.95±0.1eV3存在1.27电子伏特的偏差。目前尚无其他理论或实验IP数据可供比对。我们期待未来能开展更多实验研究和/或其他更高阶的理论计算工作。
As₆及其带电分子。对于中性的As₆,先前的研究[7,27,30]表明,有两种低能态结构的能量非常接近。一种是具有C₂ᵥ对称性和¹A₁态的苯并瓦伦(benz - valene)结构,另一种是具有D₃ₕ对称性和¹A₁′态的三棱柱结构,分别如图5a和图5b所示。沃伦(Warren)等人[27]报告称,在HF/6 - 311G**水平下,三棱柱结构的能量比苯并瓦伦结构低0.24 eV。赵(Zhao)等人[7]也指出,在DFT - PBE/DND水平下,三棱柱结构在能量上比苯并瓦伦结构稳定0.13 eV。相反,巴洛内(Ballone)等人[30]报告称,在LSD - DC水平下,苯并瓦伦结构比三棱柱结构略微稳定0.06 eV。郭(Guo)[6]提出,在B3LYP/6 - 311 + G(d)水平下,As₆的基态结构是三棱柱结构。我们同样进行了B3LYP/6 - 311 + G(d)计算,发现三棱柱结构的能量实际上比苯并瓦伦结构高0.08 eV。在G3水平下,苯并瓦伦结构和三棱柱结构的能量几乎相同(苯并瓦伦结构在能量上比三棱柱结构略微不稳定0.001 eV)。
As₆的势能面非常平缓,可能存在许多异构排列,并且对平衡几何结构的准确预测需要先进的量子力学研究。

图5.中性与带电As₆0-1-1)几何结构通过MP2(全)方案和6-31G(d)基组进行优化。键长以埃为单位。相对能量△E在G3水平下未使用零点能校正,单位为电子伏特。
在G3理论水平下,带负电荷的离子As6的最低能量结构被预测为具有C2v对称性的苯并戊二烯型构型,其基态为2A2(如图5c所示)。这一结果与郭教授先前报道的结果一致。6 2A200态的D3h三角棱柱结构(如图5d所示)比基态能量略高0.05eV,理论电子能量预测值为2.08eV。目前尚无实验数据可供对比。
对于带正电荷的离子As6+,图5e-g展示了三种异构体。结构(e)呈现苯并戊烯型构型,具有C2v对称性且处于2B1基态。异构体(f)展现Cs对称性并处于2A00电子态,其能量比基态结构(e)高出0.20 eV。异构体(g)则具有C2h对称性,并处于2Ag电子态。
Guo6报告称,该体系在B3LYP/6-311+G(d)理论水平下处于基态。在G3理论水平下,它仅是势能面上的局域最小值。从能量角度看,其稳定性比基态(e)低0.79电子伏特。理论预测的IP值为7.97电子伏特。目前尚无实验数据可供比较。
As7及其带电分子结构。图6展示了中性砷七的两种最低能量结构、阴离子态砷七的两种结构以及阳离子态砷七+的一种结构。对于中性砷七,其中一种结构(图6a)可视为用砷原子包裹砷六(As6)的三角棱柱;另一种结构(图6b)则可视为用砷原子包裹苯并二甲苯型砷六。被包裹的三角棱柱结构呈现C2v对称性且处于2B1状态,而被包裹的苯并二甲苯异构体则具有Cs对称性且处于2A0状态。从能量角度看,C2v结构仅比Cs结构稳定0.02电子伏特,这表明
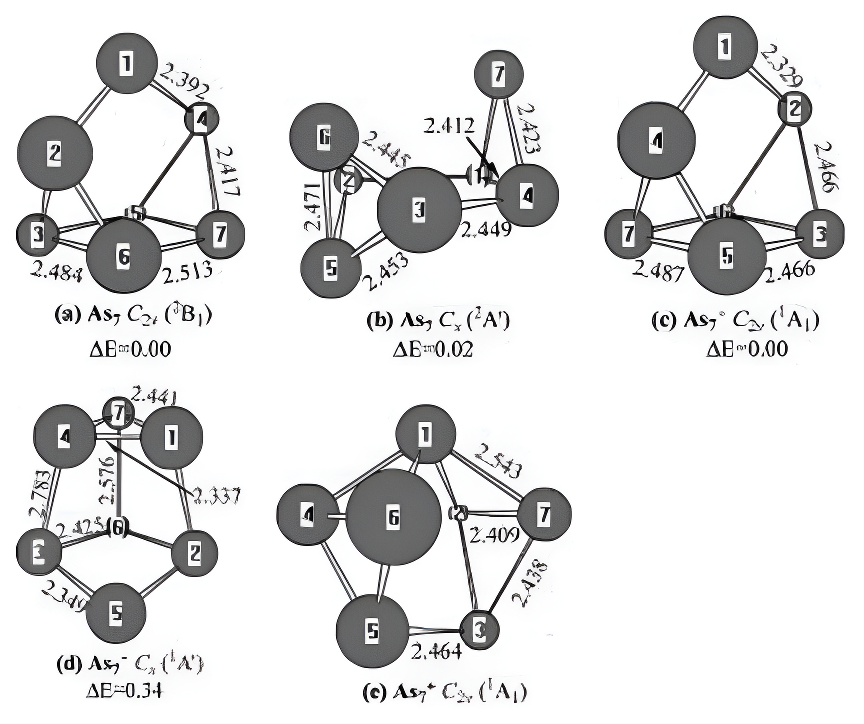
图6.中性及带电AsO-1(+1)几何构型通过MP2(全)方案和6-31G(d)基组进行优化。键长单位为埃。相对能量(△E)在G3水平下未使用零点能校正,单位为电子伏特。
As₇的势能面非常浅。在B3LYP/6 - 311 + G(d)理论水平下,戴帽三角棱柱结构也是能量最低的结构。
给中性As₇的戴帽三角棱柱结构附上一个电子会形成具有C₂ᵥ对称性和¹A₁电子态的阴离子As₇⁻(图6c),这是基态结构。这一结果与B3LYP/6 - 311 + G(d)的结论一致。
从能量上看,Cₛ结构比C₂ᵥ结构稳定性低0.34 eV。理论预测的电子亲和能(EAs)为2.93 eV。没有实验值可供对比。
对于带正电的离子As₇⁺,图6e所示的基态结构具有C₂ᵥ对称性和¹A₁基态。这一结果与B3LYP/6 - 311 + G(d)的结论一致。理论预测的电离能(IP)为6.58 eV。没有实验值可供对比。
As₈及其带电分子。对于中性As₈,存在两种极小值结构。图7a所示的双四面体结构可以看作是在As₆的苯并瓦烯结构上附上两个砷原子。图7b所示的笼状结构可以看作是在As₆的三角棱柱结构上加上两个砷原子。前者具有C₂ₕ对称性和¹A₉基态,后者具有C₂ᵥ对称性和¹A₁电子态。从能量上看,C₂ₕ结构比C₂ᵥ结构稳定性高0.09 eV。这些结果与密度泛函理论(DFT)的结果不同。在PBE和LSD理论水平下,C₂ᵥ笼状异构体在能量上分别比双四面体结构稳定0.32 eV和0.57 eV。
对于带负电的离子As₈⁻,图7c和图7d展示了两种异构体。结构(c)和(d)都具有Cₛ对称性和²A″电子态。从能量上看,在G3水平下,前者(基态结构)比后者稳定性高0.30 eV。这一结果与郭等人先前的研究结果不同。
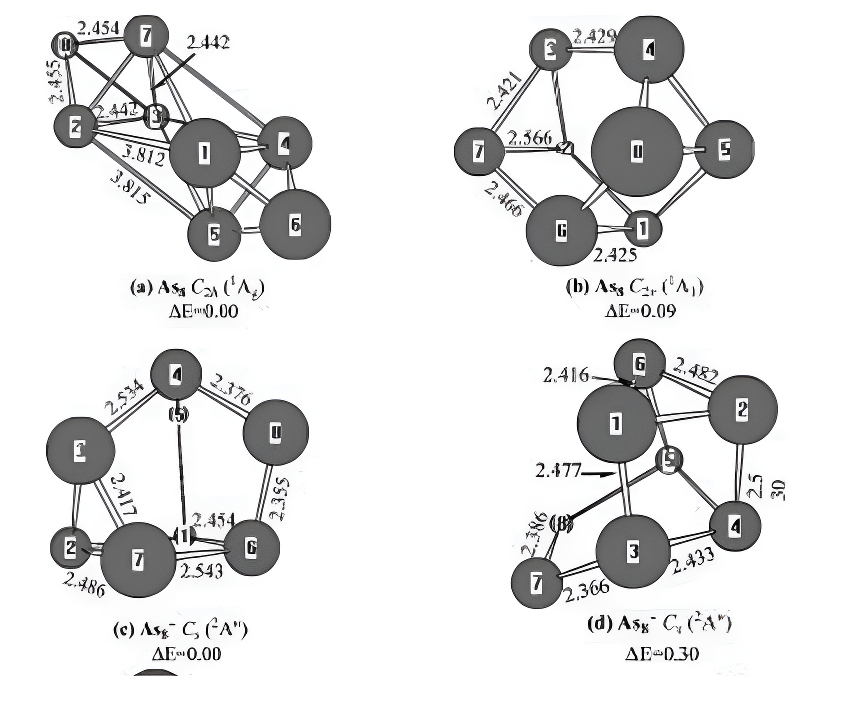
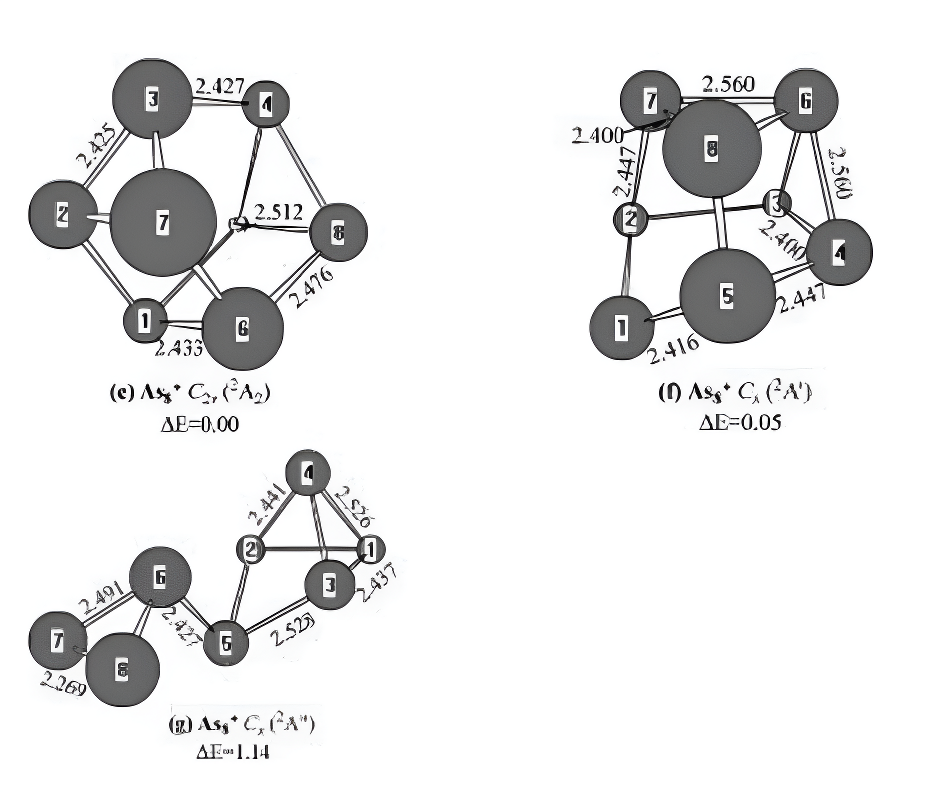
图7.中性及带电As₂0-1,+1)几何结构通过MP2(全)方案和6-31G(d)基组进行优化。键长以埃为单位。相对能量△E在G3水平下未使用零点能校正,单位为电子伏特。
预计为2.02 eV。没有可供比较的实验值。
对于带正电荷的As8+离子,图7e-g展示了三种异构体。笼状结构(图7e)呈现C2v对称性,对应2A2基态电子构型。图7f所示异构体具有Cs对称性,对应2A0电子态。从能量角度看,其稳定性仅比基态结构低0.05eV。图7g的异构体则呈现Css对称性,对应2A00电子态。郭等人曾报道图7中的结构(g)是阳离子As8+的基态,但其稳定性比2A2基态结构低1.14eV。理论预测的IP值为7.65eV,目前尚无实验数据可供对比。
值得注意的是,从n≥6开始,两种结构模式在竞争中性Asn的基态结构。一种来源于As6的苯并戊烯形式,另一种则源自As6的三角棱柱结构。
表2.Asn(n=2-8)的总结合能(BE)和原子结合能(BEPA)
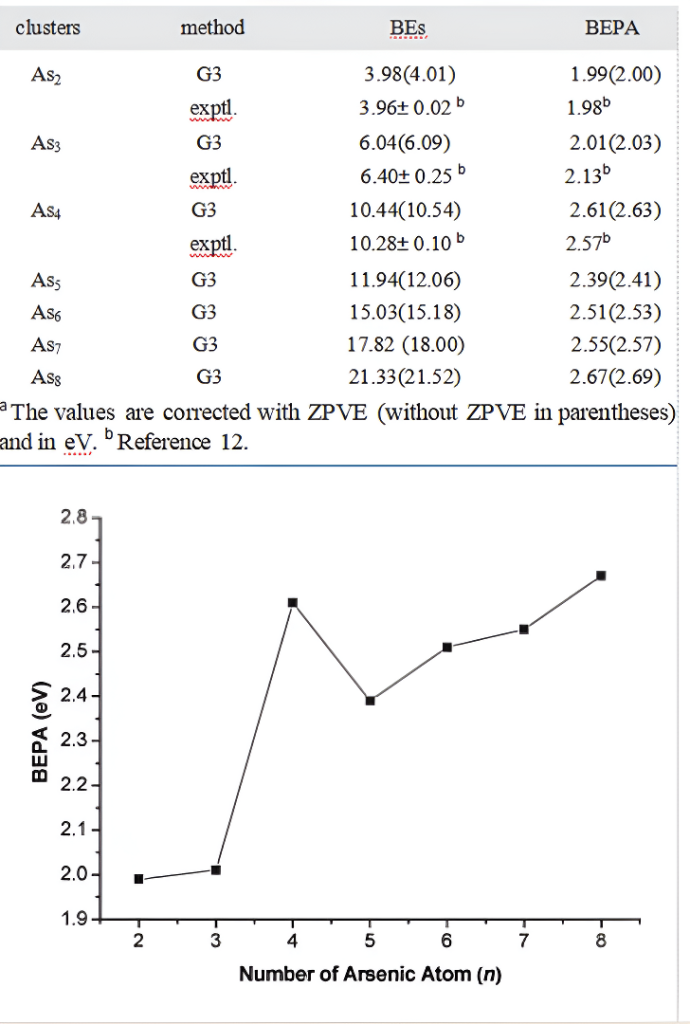
图8. 经零点振动能(ZPVE)校正后的每个原子的结合能(BEPA)(eV)与砷团簇Asₙ(n = 2 - 8)中原子数n的关系。
结合能。计算了Asₙ的结合能(定义为反应Asₙ → nAs所需的能量,即BE(Asₙ) = [nE(As) - E(Asₙ)]),并列入表2。实验测得的结合能为:As₂的结合能是3.96 ± 0.02 eV,As₃的结合能是6.40 ± 0.25 eV,As₄的结合能是10.28 ± 0.10 eV。采用G3方法计算得到的As₂、As₃和As₄的结合能分别为3.98 eV、6.04 eV和10.44 eV,与文献12中的实验值相当吻合。用G3方法预测得到的可靠结合能为:As₅的结合能是11.94 eV,As₆的结合能是15.03 eV,As₇的结合能是17.82 eV,As₈的结合能是21.33 eV。
除了总结合能之外,考虑每个原子的结合能(BEPA)对于比较不同团簇的稳定性也很有帮助。Asₙ的每个原子的结合能也列于表2中。从表2可以看出,G3方法计算得到的每个原子的结合能与实验值的偏差为:As₂偏差 - 0.01 eV,As₃偏差0.12 eV。
表3. Asₙ(n = 2 - 8)的解离能(DEs)
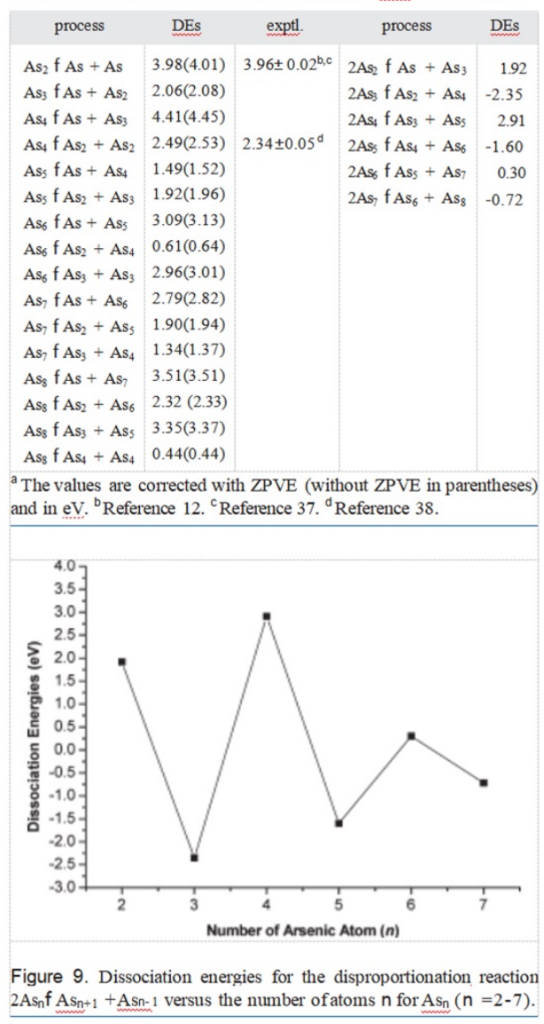
解离途径列于表3。从表3中可以看出,对于n = 5 - 8的Asₙ团簇,将其裂解成较小碎片所需的最小能量对应于过程Asₙ → As₄ + Asₙ₋₄。在G3水平下,As₅ - As₈的此类解离能分别为1.49、0.61、1.34和0.44 eV。
其他解离能(定义为歧化反应2Asₙ → Asₙ₊₁ + Asₙ₋₁所需的能量,即ΔE(Asₙ) = [E(Asₙ₊₁) + E(Asₙ₋₁) - 2E(Asₙ)])也列于表3中,并在图9中展示。这为相对稳定性提供了一个灵敏的衡量标准。
图9重现了郭等人[6]报道的结论(团簇尺寸分布呈现出明显的奇偶交替现象)。n = 2、4和6的偶数团簇比n = 3、5和7的奇数团簇更稳定。简单的解释是,偶数团簇是闭壳层体系,而奇数团簇是开壳层体系[6]。团簇稳定性的另一个衡量标准是解离能,ΔE(Asₙ) = [E(Asₙ₋₁) + E(As) - E(Asₙ)]

定义为反应 Asnf → Asn - 1 + As 所需的能量。这在图 10 中绘出。从图 10 可以看出,它还表明偶数原子团簇比奇数原子体系更稳定。
结论
我们采用G3理论方案系统研究了中性及带电小Asn(-1,0,+1)簇(n=2-8)的结构与能量特性。通过计算电子势a区nities、电离势、结合能及解离能,并与有限实验数据进行对比,得出以下结论:(i)中性Asn簇的势能面极为平缓,在n≥6的Asn基团中存在两种竞争性结构模式。其中一种源自As6的苯并戊二烯构型,另一种则源于As6的三角棱柱结构。(ii)基于G3理论模型,我们重新解析了文献1中报道的As3光电子谱。实验测得As3的电子a区nities为1.81 eV,而非文献1中的1.45 eV。根据G3和密度泛函理论结果,我们认为文献4中As5的可靠电子☒数(3.51 eV)存在误差。经预测,As2的可靠电子a区nities为0.83 eV,As3,0.54eV的As4为1.80 eV,As5为3.01 eV,As6为2.08 eV,As7为2.93 eV,As8为2.02 eV。(ii)G3理论计算得到As2电离势为9.87 eV,As3为7.33 eV,As4为8.65 eV,As5为6.68 eV,As6为7.97 eV,As7为6.58 eV,As8为7.65 eV。这些理论值对应于As2、As3等原子的电离势分析。(四)计算了总结合能和单原子结合能。经计算,As2的单原子结合能为1.99电子伏特,As3为2.01电子伏特,As5 forAs4,2.39 2.61电子伏特,As6为2.51电子伏特,As7为2.55电子伏特,As8则达到2.67电子伏特。其中As2、As3和As4的数值与实验结果高度吻合。(五)通过解离能分析考察相对稳定性,结果显示偶数个原子组成的团簇比奇数个原子的系统更稳定。
我们希望我们的理论预测将为进一步实验研究这些重要的砷团簇提供强大的动力。
作者信息
真:86 - 471 - 6576145。电子邮件:yangic@i - mut.edu.cn。
致谢
本工作得到了以下资助:国家自然科学基金项目(编号:40572149 和 40772162)、国家重点基础研究发展计划(973 计划)基金项目(编号:2006CB202205)以及国家“十一五”科技支撑计划项目(编号:2007BAK24B01 和 2006BAB16B04)。
参考文献
(1)利帕,T.P.;徐,S.-J.;利亚普斯季娜,A.;尼尔斯,J.M.;
鲍文,K.H.《化学物理学报》1998年,第109卷,第10727页
(2)阿尔卡米,M.;M,O.;Y《化学物理学报》1998年,第108卷,第8957页
(3)齐默尔曼,J.A.;巴赫,S.B.H.;沃森,C.H.;艾勒,J.R.
《物理化学杂志》1991年,第95卷,第98页
(4)翟,H.-J.;王,L.-S.;库兹涅佐夫,A.E.;博尔迪列夫,A.I.《物理化学杂志A》2002年,第106卷,第5600页。
(5)沃尔特,C.W.;吉布森,N.D.;菲尔德,R.L.;
斯内登,A.P.;夏皮罗,J.Z.;扬恰克,C.M.;汉斯托普,D.《物理评论A》2009年,第80卷,第014501页。
(7)赵,J.;周,X.;陈,X.;王,J.;耶利内克,J.《物理评论B》2006年,第73卷,第115418页。
(8)赵,Y.;徐,W.;李,Q.;谢,Y.;谢弗,H.F.《计算化学杂志》2004年,第25卷,第907页。
(9)沈,M.;谢弗,H.F.《化学物理学报》1994年,第101卷,第2261页。
(10)柳,R.K.;鲁斯西奇,B.;伯科维茨,J.《化学物理学报》1992年,第96卷,第6696页。
(11)巴拉苏布拉马尼亚姆,K.;苏马蒂,K.;戴,D.《化学物理学报》1991年,第95卷,第3494页。
(12)贝内特,S.L.;马格雷夫,J.L.;富兰克林,J.L.;哈德森,J.E.《化学物理学报》1973年,第59卷,第5814页。
(13)徐,W.;李,G.;于,G.;赵,Y.;李,Q.;谢,Y.;谢弗,H.F.《物理化学杂志A》2003年,第107卷,第258页。
(14)卡萨洛夫,V.;谢弗,H.F.《计算化学杂志》2005年,第26卷,第411页。
(15)董,C.;杨,J.;宁,H.;李,C.《分子结构:理论化学》2010年,第958卷,第26页。
(16)高,A.;李,G.;常,Y.;陈,H.;李,Q.
《分子结构:理论化学》2010年,第961卷,第88页。
(17)高,A.;李,G.;常,Y.;陈,H.;芬洛,
D.;李,Q.《无机化学学报》2011年,第367卷,第51页。
(18)柯蒂斯,L.A.;拉加瓦查里,K.;雷德芬,P.C.;拉索洛夫,V.;
J.A.《化学物理学报》1998年,第109卷,第7764页。
(19)柯蒂斯,L.A.;雷德芬,P.C.;拉索洛夫,V.;凯齐奥拉,G.;波普尔,J.A.《化学物理学报》2001年,第114卷,第9287页。
(20)巴蒂亚,K.S.;琼斯,W.E.《加拿大物理学杂志》1971年,第49卷,第1773页。
(21)王,L.S.;李,Y.T.;雪莉,D.A.;巴拉苏布拉马尼亚姆,K.;冯,P.《化学物理学报》1990年,第93卷,第6310页。
(22)王,L.S.;牛,B.;李,Y.T.;雪莉,D.A.;盖利奇卡尼,E.;格兰特,E.R.《化学物理学报》1990年,第93卷,第6318页。
(23)王,L.S.;牛,B.;李,Y.T.;雪莉,D.A.;盖利奇卡尼,E.;格兰特,E.R.《化学物理学报》1990年,第93卷,第6327页。
(24)布伦巴赫,S.B.;罗森布拉特,G.M.《化学物理学报》1972年,第56卷,第3110页。
(25)斯库塞里亚,G.E.《化学物理学报》1990年,第92卷,第6722页。
(26)迈尔,U.;佩耶里姆霍夫,S.D.;格林,F.《化学物理》1991年,第150卷,第331页。
(27)沃伦,D.S.;吉马克,B.M.;赵,M.《无机化学》1994年,第33卷,第710页。
(28)贝尔布鲁诺,J.《杂原子化学杂志》2003年,第14卷,第189页。
(29) 伊格尔 - 曼恩,G.;斯托尔,H.;普雷斯,H.《分子物理学》1993 年,80 卷,325 页。(30) 巴洛内,P.;琼斯,R.O.《化学物理学报》1994 年,100 卷,4941 页。(31) 巴鲁阿,T.;佩德森,M.R.;佐普,R.R.;贝尔特兰,M.R.《化学物理通讯》2004 年,387 卷,476 页。(32) 弗里施,M.J.;特鲁克斯,G.W.;施莱格尔,H.B.;斯库塞里亚,
G.E.;罗布,M.A.;切斯曼,J.R.;蒙哥马利
J.A.,Jr.;弗雷文,T.;库丁,K.N.;布兰特,J.C.;米拉姆,J.M
艾扬格,S.S.;托马西,J.;巴罗内,V.;门努奇,B.;科西,M.;斯卡尔马尼,G.;雷加,N.;彼得森,G.A.;中辻,H.;哈达,M.;江原,M.;丰田,K.;福田,R.;长谷川
石田,M.;中岛,T.;本田,Y.;北尾,O.;中井,H.;克莱内
M.;李,X.;诺克斯,J.E.;赫拉奇安,H.P.;克罗斯,J.B.;巴肯,V.;阿达莫,C.;哈拉米略,J.;贡珀茨
R.;斯特拉特曼,R.E.;亚济耶夫,O.;奥斯汀,A.J.;卡米,R.;波梅利,C.;奥奇特尔斯基,J.W.;阿亚拉,P.Y.;诸熊,K.;沃思,G.A.;萨尔瓦多,P.;丹嫩贝格,J.J.;扎克热夫斯基,V.G.;达普里希,S.;丹尼尔斯,A.D.;斯特雷恩,M.C.;法卡斯,O.;马利克,D.K.;拉布克,A.D.;拉加瓦查里,K.;福雷斯曼,J.B.;奥尔蒂斯,J.V.;崔,Q.;巴布尔,A.G.;克利福德,S.;乔斯洛维斯基,J.;斯特凡诺夫,B.B.;刘,G.;利亚申科,A.;皮斯科尔兹,P.;科马罗米,I.;马丁,R.L.;福克斯,D.J.;基思,T.;阿拉 - 拉哈姆,M.A.;彭,C.Y.;纳纳亚卡拉,A.;查拉科姆比,M.;吉尔,P.M.W.;约翰逊,B.;陈,W.;黄,M.W.;冈萨雷斯,C.;波普尔,J.A.《高斯 03》,修订版 C.02;高斯公司:美国康涅狄格州沃灵福德,2004 年。
(33) 范,H.;杨,J.;陆,W.;宁,H.;张,Q.《物理化学杂志 A》2010 年,114 卷,1218 页。(34) 胡贝尔,K.P.;赫茨伯格,G.《分子光谱与分子结构。IV. 双原子分子常数》;范诺斯特兰德 - 莱因霍尔德公司:纽约,1979 年。(35) 森野,Y.;宇贺地,T.;伊藤,T.《日本化学会通报》1966 年,39 卷,64 页。(36) 里恩斯特拉 - 基拉科菲,J.C.;楚姆珀,G.S.;舍费尔,H.F.;南迪,S.;埃里森,G.B.《化学评论》2002 年,102 卷,231 页。(37) 赫尔特格伦,R.;奥尔,R.L.;凯利,K.K.《金属和合金热力学性质选定值补编(砷)》;加利福尼亚大学:加利福尼亚州伯克利,1970 年 8 月。(38) 默里,J.J.;普普,C.;波蒂,R.F.《化学物理学报》1973 年,58 卷,2569 页。.

